DANIELA DUQUE AREA: MATEMATICAS

LÓGICA MATEMÁTICA

La lógica matemática es una parte de la lógica y las matemáticas que consiste en el estudio matemático de la lógica y en la aplicación de este estudio a otras áreas de las matemáticas. La lógica matemática tiene estrechas conexiones con las ciencias de la computación y la lógica filosófica.

La lógica matemática estudia los sistemas formales en relación con el modo en el que codifican o definen nociones intuitivas de objetos matemáticos como conjuntos, números, demostraciones y algoritmos, utilizando un lenguaje formal.

La lógica matemática suele dividirse en cuatro subcampos: teoría de modelos, teoría de la demostración, teoría de conjuntos y teoría de la recursión. La investigación en lógica matemática ha jugado un papel fundamental en el estudio de los fundamentos de las matemáticas. Actualmente se usan indiferentemente como sinónimos las expresiones: lógica simbólica (o logística), lógica matemática, lógica teorética y lógica formal.

La lógica matemática no es la «lógica de las matemáticas» sino la «matemática de la lógica». Incluye aquellas partes de la lógica que pueden ser modeladas y estudiadas matemáticamente.

CONCEPTO DE LÓGICA MATEMÁTICA

La lógica matemática estudia los sistemas formales en relación con el modo en el que codifican conceptos intuitivos de objetos matemáticos como conjuntos, números, demostraciones y computación. La lógica estudia las reglas de deducción formales, las capacidades expresivas de los diferentes lenguajes formales y las propiedades metalógicas de los mismos.

En un nivel elemental, la lógica proporciona reglas y técnicas para determinar si es o no válido un argumento dado dentro de un determinado sistema formal. En un nivel avanzado, la lógica matemática se ocupa de la posibilidad de axiomatizar las teorías matemáticas, de clasificar su capacidad expresiva, y desarrollar métodos computacionales útiles en sistemas formales. La teoría de la demostración y la matemática inversa son dos de los razonamientos más recientes de la lógica matemática abstracta. Debe señalarse que la lógica matemática se ocupa de sistemas formales que pueden no ser equivalentes en todos sus aspectos, por lo que la lógica matemática no es método de descubrir verdades del mundo físico real, sino sólo una fuente posible de modelos lógicos aplicables a teorías científicas, muy especialmente a la matemática convencional.

La lógica matemática no se encarga por otra parte del concepto de razonamiento humano general o del proceso creativo de construcción de demostraciones matemáticas mediante argumentos rigurosos pero hechas usando lenguaje informal con algunos signos o diagramas, sino sólo de demostraciones y razonamientos que pueden ser completamente formalizados en todos sus aspectos. 

LÓGICA DE PREDICADOS 

La lógica de predicados (o lógica de primer orden) es un lenguaje formal en el que las sentencias bien formadas son producidas por las reglas enunciadas a continuación.

Vocabulario

Un vocabulario es una tupla: 

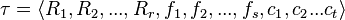 que consta de:

•  símbolos relacionales , cada uno de ellos con un número entero  asociado, el cual se conoce como la arridad de 
•  símbolos funcionales 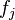, cada uno de aridad 
•  símbolos constantes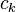 

Una fórmula de primer orden  en el vocabulario , es una fórmula de primer orden donde los únicos predicados, funciones y constantes empleados son los especificados por 

EJERCICIOS 

Problema de razonamiento numérico

Un grupo de 3 amigos organiza la rifa de una bicicleta con valor de $1, 900.00, para poder realizar
un viaje  de $1, 425.00 por persona. Si el boleto de la rifa cuesta $75.00, ¿cuántos boletos deberán
vender para  poder hacer el viaje, considerando que deben recuperar la inversión?

a) 76

b) 64

c) 83

d) 57

David tiene libros en diferentes idiomas. Se sabe que todos menos tres son libros en alemán, que  todos menos tres son libros en italiano y que todos menos tres son libros en francés. El resto son  libros en español. ¿Cuántos libros en español tiene David?

a) 4

b) 3

c) 2

d) 1